Perdonami ancora, te parlavi genericamente di velocità, il report parla di velocità media.
Ora, il primo ed il secondo sono sostanzialmente differenti.
Una velocità istantanea da 50 kmh ijn città è possibile, una velocità media a 50 kmh in città è impossibile.
E sempre dal report menzionato, lo stesso grafico, data la velocità media in città che di rado supera i 20kmh, la differenza di consumo è risibile, ed è parecchio influenzata dalla marcia che tieni.
Sempre dal medesimo report, la fig 2 imho è anomala, se guardiamo il rapporto marcia consumi
Vedi l'allegato 31016
Sono supposizioni soggettive.
Parliamo della media, partiamo dai fondamenti di matematica delle medie.
Parlare di media non vuol dire nulla, è un numero che di fatto non da particolari indicazioni, se non viene associato allo scarto quadratico medio.
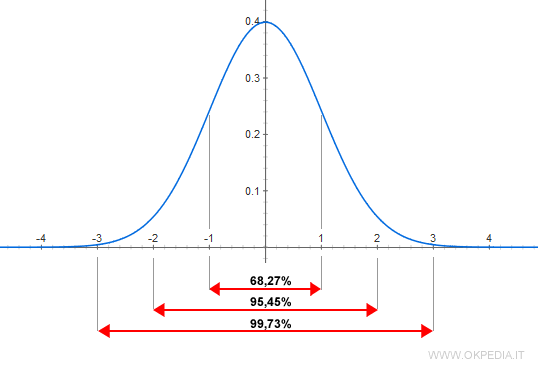
Se non viene associato alla media la distribuzione dei dati (scarto quadratico medio) normalmente si intende la normale distribuzione e scostamento detta
Gaussiana (vedi fig2),
ed il 70% dei dati è attorno al valore numerico mediano.
Lo scarto quadratico medio ci aiuta a stabilire se e quanto i dati
sono concentrati o dispersi intorno alla loro media e quanto la media sia significativa.
Per quasi tutti gli insiemi di dati, la maggior parte dei valori osservati si trova nell'intervallo centrato sulla media e i cui estremi distano dalla media per 1 scarto quadratico medio.
Parliamo di deviazione standard
Data una distribuzione statistica X composta da N valori numerici, la deviazione standard è la radice quadrata della media aritmetica degli scarti assoluti tra i valori della distribuzione { x1, x2, ... , xN} e un valore medio ( μ ).
Esempi con 4 dati
Caso 1) 50, 50, 50, 50 media uguale a 50
caso 2) 99, 1, 70, 30 media uguale a 50
E’ chiaro che pur avendo la stessa media non è la stessa distribuzione di dati e sono statisticamente diversi lo scarto quadratico medio nel primo caso è 0 (zero)
Nel secondo caso è 10,58
Quindi la prima è una media significativa la seconda meno, ha troppa dispersione.
Bene ora siamo in grado di stabilire che nella prima i valori numerici osservati sono tutti uguali alla media, nel secondo caso, la media è molto meno significativa poiché lo scarto quadratico è elevato.
Quindi nel caso che si parli di media come ho detto sopra si intende una deviazione standard con il 70 % dei valori al centro della gaussiana ed il 95% con scarto quadratico medio 2 (due).
Quindi average speed i valori numerici rilevati sono al 70/80% vicini al valore medio ed il 95% con scarto 2 (due).
Per chi vuole approfondire un libro delle medie inferiori
Matematica di base: Aritmetica e pre-algebra (partendo da zero) (Ottavio Calzone)